Psikolojinin Matematik Bilimiyle İlişkisi ( İstatistik Metot)

Psikolojik fenomenler sayısal olabildikleri ölçüde, bu sayısal sonuçları açıklamak için matematik aracın kullanılması kaçınılmaz olur. Psikolojide kullanılan matematiğe ait branş hemen hemen yalnızca ihtimaller hesabıdır.

Psikolojik fenomenler genellikle birçok değişkenlere bağlıdır. Deney metodu, bütün değişkenleri, birisi hariç olmak üzere sabit tutmaktan ibarettir. Bu da incelenmek istenen değişkendir. Fizik ilimlerinde bu nispeten kolay olmakla beraber psikolojide değişkenlerin kontrolü ancak ihtimalidir.

Öğrenme kanunlarını incelemek istediğimizde, bunu yapmak için, bir süjenin bir metni hatasız olarak tekrarlamaya kabiliyetli olup olmadığını anlamak üzere, gerekli metni okuma sayısını hesap ederiz, tespit edeceğiz ki, daima aynı şartlar içinde çalışma tedbiri alsak ve mümkün olduğu kadar birbirine benzeyen süjeler üzerinde çalışsak bile (mesela. Aynı cinsten, aynı yaştan, aynı kültür seviyesinden), bu sayı fertten ferde değişecektir.

Kontrol ettiğimiz değişkenler önemli olmakla beraber, bahis konusu olan yalnız onlar değildir. Esasen kat’i sayısını ve tabiatını bilmediğimiz kontrol edilmeyen birçok değişkenler vardır. Bu şartlarda ihtimaliyet kanunlarını takip ederek dağılan bu değişkenlerin aksiyonunu hipotez yapabiliriz, bir miktar süjenin sonuçlarının ortalamasını aldığımızda bu ortalama sonuç kontrol edilmemiş değişkenlerden bağımsız olacaktır.

Psikolojik olduğu kadar biyolojik bütün beşeri ilimlerde durum, esasen hundan farklı olmayacaktır. Büyük miktarların kanununa başvurma, değişmez sonuçlar almak için tek vasıtadır. Bir miktar fertten elde edilen neticeler ölçü çizelgesinin bir kısım alanına dağılırlar.

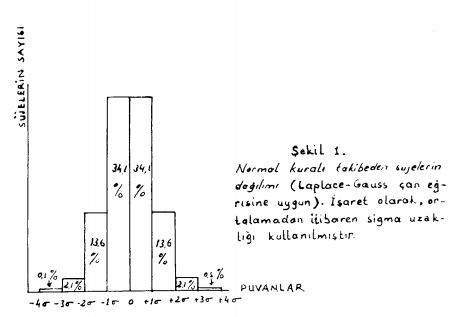
Dikey çizgide, her değerin nitelediği süje sayısı, değerler çizgisine uzatıldığı zaman çan şeklinde gösterildiği gibi, matematikçilerden iki kişinin adıyla anılan Laplace-Gauss eğrisi adı verilen bir eğri elde edilir.

Bu eğri, bir ortalama (alışıldığı şekilde aritmetik ortalama kullanılır) ve bir dağılım işareti (alışıldığı şekilde alınan sonuçların, ortalamanın etrafında dağılma nispetini gösterim sigma işareti kullanılır) vasıtasıyla belirlenmiştir.

Laplace-Gauss eğrisi

Bu dağılım işareti, eğrinin hangi ölçüde az veya çok bir basıklığa (yayvanlığa) sahip olduğunu işaret eder, yani sonuçların ortalama etrafında hangi nispette dağılmış olduğunu belirtir.

Artık sadece bir değişken değil (öğrenme hızı gibi), fakat aynı zamanda beraberce iki değişken incelendiği zaman istatistik korelasyon kavramına baş vurulur. Aynı anda öğrenme hızını ve mesela kendimize has bir denemeyle kültür seviyesini ölçtüğümüz bir süje gurubu farz edelim. İki değişken arasındaki ilişkileri inceleyebiliriz. Beraber değişme (covariation) derecelerini araştırabiliriz.

Aradaki süreler her iki deneme sonuçlarında aynı karşılıklı yeri işgal ederek eğer, çok zeki olan süre çok çabuk öğreniyorsa ve eğer az zeki olan süre geç öğreniyorsa diyeceğiz ki, iki deneme mükemmel bir tarzda müspet olarak ilişkili (correle) dirIer. Aksine eğer tasnifler arasında hiçbir ilişki yoksa diyeceğiz ki, iki değişken kendi aralarında menfi bir korelasyona sahiptirler.

Bu ilişkinin kuvvetini korelasyon katsayısı veya sayısal bir işaretle ifadenin çeşitli yolları vardır.

Psikolojik gözlemde iki değişken arasındaki müspet bir korelasyonun meydana çıkması çeşitli tefsirlere elverişlidir. Hiçbir zaman bir sebep-netice ilişkisi bahis konusu değildir. Çok defa, ortaya çıkmış olan korelasyon. İncelenmiş iki değişkenin bir üçüncü ortak değişkenin bağımlılığı altında olmasından ileri gelir.

Böylece fizik sahada, bir çocuğun boyu ile ağırlığı arasında müspet bir korelasyon vardır. Bu, özellikle her ikisinin olgunlaşma ve yaşın fonksiyonu olmaları gerçeğinden ortaya çıkar. Ölçülebilen değişkenlerden çok sayıda mevcut olduğu zaman ikişer ikişer alınan bu değişkenlerin arasındaki korelasyonlar bir gurup fert üzerinde hesaplanabilir.

Böylece, kalıp (matrice) denilen bir korelasyon ağı elde edilir. değişkenlerin tümü üzerine aynı anda etkide bulunan mahdut sayıda faktörlere baş vurarak. Bu korelasyonları basit tarzda ortaya çıkarmaya imkan veren matematik yöntemler vardır. Bu kompleks metotlar faktör analizi (analyse factorielle) adını alır.

Psikolojide kullanılmış olan istatistik metotlar, ister tecrit edilmiş değişkenler olsun, ister aynı anda birçok değişkenler olsun bunları incelemeye ve bu suretle çok basit ve kesin bir dille gözlemleri açıklamaya imkan verirler.